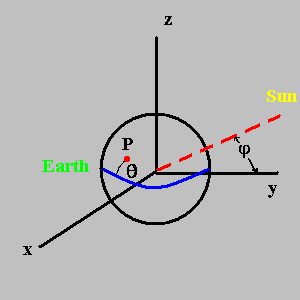

| The Earth is centered at
the origin at (0, 0, 0) and the sun is far away in the yz-plane at a declination (angle above or below the equator) of φ from the y-axis which is a vector in the direction v1=(0, cos φ, sin φ). |
|
|---|---|
| The sun's declination
changes over the year. One can assume that the declination follows a sine curve based upon being at +23.45o on June 21 (summer), 0o on March 22 and September 21 (equinox) and -23.45o on December 21 (winter). An improved approximation was used in the program: |
|
|
φ=cos-1[cos2(τ) + sin2(τ)cos(23.45o)] |
|
| where τ is 0 on March
22, 90o on June 21, etc. Note that φ is positive
in the spring & summer and negative in the fall and winter. This improved approximation comes from thinking of the sun's declination as a great circle which comes from the intersection of a tilted plane (by 23.45o)and the sphere of radius=1. This great circle can be represented parametrically by |
|
|
v2=[cos(τ),sin(τ)cos(23.45o),sin(τ)sin(23.45o)] |
|
| The vector | |
|
v3=[cos(τ),sin(τ),0] |
|
| represents the point the
Earth is in its orbit around the sun. These two vectors are at an angle φ apart where |
|
| cos(φ)=v2•v3=cos2(τ)+sin2(τ)cos(23.45o) or φ=cos-1[cos2(τ) + sin2(τ)cos(23.45θ)] |
|
| The difference between
using φ=23.45osin(τ) or φ=cos-1[cos2(τ)+sin2(τ)cos(23.45o)] affects the declination by less than 0.062o at mid-season; for example on November 7 or February 4. At the four season changes both equations yield the same value of φ. |
|
| A point, P, on the Earth
of radius=1 is located at (0, cos θ, sin θ) at noon (T=0) where θ=latitude. |
|
| At an arbitrary time,
T(hrs), the point will be at v4=(cos θ sin t, cos θ cos
t, sin θ) where t = 15oT. This comes from rotation about the z-axis by t shown by the matrix-vector multiplication: |
|
|
|
|
| The cosine of the angle
between the two unit vectors represented by the Earth's location and the sun's location is found by the equation cos β=v1•v4 (the dot product). That is, |
|
|
cos β=[0][cos θ sin
t]+[cos φ][cos θ cos t]+[sin φ][sin θ] |
|
| The altitude, α, is given by 90o - β or cos β = sin(α). This yields: | |
| α=sin-1(sin θ sin φ + cos θ cos φ cos t) | |
| Sunrise and sunset occur
when α=0. If sin θ sin φ + cos θ cos φ cos t = 0, then cos t = -tan θ tan φ. That is, t=cos-1(-tan θ tan φ)=180o+/-cos-1(tan θ tan φ). Since time is given in hours 15o represents 1 hour. Then we can rewrite t as 12+/-cos-1(tan θ tan φ)/15o. |
|
Starting
with a vector S for the position vector of the sun: 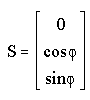 |
|
|
The Earth coordinate system x-y-z is transformed to x*-y*-z* by |
|
|
|
|
| The dot product of these x*-y*-z* vectors with S yields the following: | |
|
|
|
| Each of these
components is given in the output. The azimuth is found by looking at the x' and y' only. The azimuth, az, is rotated by 90o because it is measured from the y-axis. Therefore, |
|
|
az=tan-1(-x'/y')=tan-1(cos φ sin t/(cos θ sin φ - sin θ cos φ cos t)) |
|
| Finally, to measure the
azimuth at sunset and sunrise (these are shown as blue lines), one needs to substitute for both cos t and sin t into the equation for az. The substitutions are: |
|
|
|
|
| Then after some
trigonometric manipulation we get cos(az)=sin(φ)/cos(θ). Return to sungraph.html |